Curanz Soundsの音響技術に興味を持ってくださり
ありがとうございます
ここからはかなり専門的なページになります
サンプリング音源の有用性
Curanz Soundsのピアノシリーズは
カバー作品やオリジナル含めてこだわったピアノ音質にしております。
代表の朝比奈幸太郎の専門がピアノだということもあり
ピアノの音質にはかなりこだわって研究してきました
ただし、生ピアノをそのまま432hzや純正律で調整するのは
あまり現実的ではありません
なぜなら現代で制作されたピアノは
440hzのテンションを適正と定義して作られているため
8hz落として調律するとそのテンションを維持することが難しいわけです
また、気温の変化、湿度の変化、調律師の協力やボディーの提供など含め
コスト的に難しいというのもあります
Curanz Soundsの音楽ホールが完成した際には
生のグランドピアノを432hzで調整したコンサートを提供します

現在はこだわり抜いたサンプリング音源を使っています。
YAMAHAのフルコンサートグランドをドイツの老舗音響スタジオにて何十個、何百個のマイクロフォンで1音ずつサンプリングした音源を使用しており、実質生録と変わりないものに仕上げることができるどころか、音響システムとしてもマイクロフォン、マイクアンプにADCなど、個人で用意できる機材を遥かに超えたシステムでサンプリングしているため、安定して音響を供給するためにはこちらの方がむしろベストな選択肢であるとさえ言えます。
また、近年のコンピューター性能の向上から、レイテンシも限りなくゼロに近い状態を維持できますので、演奏家としてのパフォーマンスも低下することなく皆様に最高水準の音響と演奏を提供できるわけです。
アナログをデジタルに変換
ここでいうサンプリング音源とは上記で示した通り、ほとんど生録音と変わりありません。
アナログ-デジタル変換(ADC)プロセスは、アナログ信号をデジタル信号に変換する重要なステップとしては主に3つのステップで構成されています。
- サンプリング:連続的なアナログ信号を特定の時間間隔で測定し、離散的なサンプルに変換します。
- 量子化:各サンプルのアナログ値を固定された数値の範囲(量子化レベル)にマッピングします。
- 符号化:量子化された値をデジタルビット列に変換します。
サンプリング
シャノンのサンプリング定理によれば、信号を正確に再構築するためには、サンプリング周波数が元の信号の最高周波数の2倍以上でなければならないとされています。
この条件を満たすサンプリング周波数をニクイスト周波数と呼びます。
量子化
量子化プロセスでは、連続的なアナログ値を固定された数値の範囲にマッピングしていきます。
量子化ステップ(Δ)は、信号の最小値と最大値の範囲を量子化レベルの数で割ることにより決定されます。
量子化誤差は、実際のアナログ値と量子化された値との差です。
量子化ビット数(nビット)を増やすと、量子化誤差は減少しますが、データのビット数が増加します。
量子化された値はデジタルビット列に変換され、各量子化レベルは固有のビットパターンに対応します。例えば、8ビットのADCでは、量子化レベルは256(2828)あり、0から255までの値を持つことができます。
ADCの計算式
サンプリング定理の基本式は以下の通りです:

このようなプロセスを録音技術を持っても同様に行った後、処理されたデジタルデータとして取り扱うため、生録とサンプリング音源の差はほとんどありません。
セイビンの法則でのリバーブ演算処理のコード
さて、サンプリングされた音源の唯一の弱点となるのが、空間の振動を捉えられない(録音)という点にあります。
これははっきりいって明らかに生演奏の方が優位性が高いと断言できます。
ただし、デジタルオーディオにおける皆様へ癒しの周波数を倍音として乗せることで擬似的に空間を演出することにつながるのです。
以下は音響の法則の一つであるセイビンの法則を使ったリバーブの演算処理のPythonコードになります。
セイゲンについてはこちらの記事でチェックしてください。
import numpy as np
def simple_reverb(signal, sample_rate, delay_seconds=0.5, decay=0.5):
"""
単純なリバーブエフェクトを信号に適用します。
Parameters:
- signal: 入力信号 (numpy array)
- sample_rate: サンプリングレート (Hz)
- delay_seconds: ディレイ時間 (秒)
- decay: 減衰率
Returns:
- 処理後の信号 (numpy array)
"""
# ディレイサンプル数を計算
delay_samples = int(sample_rate * delay_seconds)
# 出力信号用の配列を準備(元の信号よりも長い)
output = np.zeros(len(signal) + delay_samples)
# 入力信号を出力信号にコピー
output[:len(signal)] = signal
# リバーブ効果を追加
for i in range(len(signal)):
output[i + delay_samples] += signal[i] * decay
return output
# サンプリングレート(Hz)
sample_rate = 44100 # CDクオリティ
# ここで、'signal'は処理したい音源のサンプルデータをnumpy配列で与える
# 例: signal = np.random.uniform(-1, 1, sample_rate) # 1秒間のホワイトノイズ
# リバーブ処理を適用
# processed_signal = simple_reverb(signal, sample_rate, delay_seconds=0.5, decay=0.5)
# 処理後の信号 'processed_signal' を使用
リバーブ処理における減衰率(decay)の設定は、目指す残響効果の種類や音源の特性によって異なります。
ここは音響技術師の長年の勘も必要になってきます。
Curanz Soundsは音響技術者も演奏家も服部 洸太郎がになっており、長年の演奏家活動の中で様々な現場で最高のピアノを使って実験を重ねていった成果として体現しております。
もちろんこの音響技術は体現するだけではなく、追って体系化して伝えていきたいと思っております。
Curanz Soundsの協力者が現れるその日まで。
音律の計算と純正律の設定方法
古代の叡智を再現するためのピアノ演奏においては、432hz周波数に加えて音律という概念も大変重要な要素となってきます。
音律は432hzにおける純正律とピタゴラス音律の計算については、こちらもPythonコードにてpandasを用いたコードとしてまとめていますので、シェアしておきます。
ピタゴラス音律をPythonコードでメモ〜ピタゴラス教団の叡智を徹底解説
また、現在広く使用されている平均率というのは、12キーすべてで調和を満たすという、極めてピアノの世界だけの話になります。
本来の音律というのはもう少し自由でいいわけです。
平均律を世界的に採用したのはバッハですが、バッハが平均率を採用した理由も記事にまとめていますので、是非チェックしてみてください。
こちらは、叡智の圧縮コードであると考えています。
そのため、私たち現代の音楽家が解明するべき叡智なのです。
それは何も音楽理論に沿ったものである必要はないわけです。(音楽家としての私見です)
コンピューターに音律をスクリプト登録する方法
Curanz Soundsでは、Kontaktをサンプラーとして採用しております。
このKontaktのスクリプト機能を使えば、サンプリングエンジンに対して高度なカスタマイズを可能にしてくれます。
この機能を使用し、サンプルの再生方法、エフェクトの処理、そして特に音高(ピッチ)の調整をスクリプトによってある程度制御することができるわけです。
純正律で432Hzの基準音を使用して演奏する場合、以下のような手順と調整が考えられます。
純正律での音高調整
すでにいくつかの記事でもお伝えしている通り、純正律では、各音程が特定の周波数比に基づいています。
たとえば、主要三度は5:4の比率、完全五度は3:2の比率です。
Kontaktのスクリプトエディタを使用して、これらの比率に基づいて各ノートのピッチを調整するスクリプトを記述します。
スクリプトの基本的な構造
Kontaktスクリプトでは、on noteイベントを使用して、ノートが演奏されたときの動作を定義します。例えば、以下は非常に単純化されたスクリプトの例です。
on note
declare $pitchAdjustment
select($EVENT_NOTE)
case 60: $pitchAdjustment := 0 // Cの場合、調整なし
case 62: $pitchAdjustment := 0.1 // Dの場合、わずかにピッチアップ(例)
case 64: $pitchAdjustment := -0.1 // Eの場合、わずかにピッチダウン(例)
// 他のノートに対しても同様に調整を行う
end select
change_note ($EVENT_ID, $EVENT_NOTE, $EVENT_VELOCITY, $pitchAdjustment)
end on
この例では、change_note関数を使用して、演奏されたノートのピッチを微調整しています。
実際には、$pitchAdjustmentの値を正確な周波数比に基づいて計算する必要があり、これには各ノートの基準となる周波数(432Hzを基準とした周波数)を考慮に入れる複雑な計算が必要になります。
実際に純正律で432Hzを基準に演奏するには、上記のスクリプトをさらに詳細に拡張し、各ノートのピッチを正確に調整していきます。
純正律に基づく周波数比を用いて他のノートの周波数を計算していきましょう。
純正律における主要な音程の比率は以下の通りです。
- 完全五度(GからC): 3/2
- 主要三度(EからG): 5/4
- 完全四度(CからE): 4/3
これらの比率を使用して、C4の周波数を求めるましょう。
純正律でC4からA4までの関係を見ると、A4はC4から完全五度上のG4、さらに主要二度(9/8)上のA4に位置します。
したがって、A4(432Hz)から逆算してC4の周波数を求めることができます。

これらを実際にPythonで書いてみると次のようになります。
# A4の周波数を432Hzと設定
A4_frequency = 432
# A4からC4への周波数計算
G4_frequency = A4_frequency * (2 / 3) # 完全五度下
C4_frequency = G4_frequency * (3 / 4) # 完全四度下
# 純正律に基づくCメジャースケールの周波数比
intervals_ratio = {
'C': 1,
'D': 9 / 8,
'E': 5 / 4,
'F': 4 / 3,
'G': 3 / 2,
'A': 5 / 3,
'B': 15 / 8,
'C5': 2
}
# Cメジャースケールのノートと周波数の計算
notes_frequency = {note: C4_frequency * ratio for note, ratio in intervals_ratio.items()}
notes_frequency
こちらは外部ライブラリを使う必要はなく単純なPythonの標準機能だけで数値計算や辞書操作を行うことができます。
これらの考え方は他の周波数帯の音楽を制作する際にも非常に重要なポイントとなっていますので、癒しの音楽を制作する際は是非マスターしておいてください。
こちらはCメジャースケールに対する純正律のKontaktサンプルコードスクリプトです。
{ Kontaktスクリプトの例: 432Hz基準の純正律 }
on init
{ A4を432Hzとする }
set_knob($PITCH_KNOB, 0) { ピッチベンドの中心値を設定 }
declare $baseFreq := 432
declare $noteFreq[128]
declare $freqRatio[128]
declare %notes := (0, 2, 4, 5, 7, 9, 11, 12) { Cメジャースケールのノート番号 }
declare $i
{ C4の周波数を計算し、純正律に基づく周波数比を設定 }
$noteFreq[60] := $baseFreq / 2 { C4の周波数 }
$freqRatio[60] := 1 { C4は基準となるため比率は1 }
{ 他のノートの周波数比を計算 }
$freqRatio[62] := 9/8 { D }
$freqRatio[64] := 5/4 { E }
$freqRatio[65] := 4/3 { F }
$freqRatio[67] := 3/2 { G }
$freqRatio[69] := 5/3 { A }
$freqRatio[71] := 15/8 { B }
$freqRatio[72] := 2 { C5 }
{ 実際の周波数を計算 }
for $i := 0 to 127
if ($i <> 60) { C4以外 }
$noteFreq[$i] := $noteFreq[60] * $freqRatio[$i % 12]
end if
end for
end on
on note
{ ノートに応じてピッチを調整 }
if ($EVENT_NOTE < 60 or $EVENT_NOTE > 72)
ignore_event($EVENT_ID)
else
change_note($EVENT_ID, $EVENT_NOTE, $EVENT_VELOCITY, ($noteFreq[$EVENT_NOTE] - $noteFreq[60]) * 1000)
end if
end on
当然純正律ですので、他のキーで同様のスクリプトで動作しません。
各スケールのスクリプトを用意し、意図的に調整し楽曲ごとに整理していく必要があります。
Kontaktスクリプトの記述手順
- Kontaktを開く:
- Native Instruments Kontaktを開きます。
- インストゥルメントをロードまたは作成:
- 既存のインストゥルメントをロードするか、新しいインストゥルメントを作成します。
- スクリプトタブへ移動:
- インストゥルメントエディタの上部にあるタブの中から「Script Editor」または「スクリプト」タブを選択します。
- スクリプトエディタを使用:
- スクリプトエディタが開かれます。ここにKSPコードを記述します。新しいスクリプトを作成するには、エディタ内で既存のスクリプトをクリアするか、新しいスロットを追加してください。
- コードの記述:
- 提供したコード例をスクリプトエディタにコピー&ペーストします。このコードは、特定の音律に基づいて各ノートのピッチを調整するためのものです。
- コードの実行:
- コードをエディタに入力した後、「Apply」ボタンをクリックしてスクリプトを適用します。これにより、スクリプトがインストゥルメントに対して実行されるようになります。
- テストと調整:
- スクリプトの挙動をテストし、必要に応じてコードを調整します。挙動が期待通りでない場合は、コードを見直し、エラーがないか確認してください。
レコーディング技術
シングングボールやティンシャ、龍笛や笙などの神事に使用する楽器、その他のヒーリング楽器についてはサンプリング音源は使わず生録音をしております。
生録音の技術は金田式DC録音の金田明彦氏直系の弟子であるレコーディングエンジニアの五島昭彦氏のスタジオで徹底的に学んだ実績と、今もなお五島昭彦氏を顧問として、Curanz Soundsの技術部として実験や検証を続けています。
基本的には無指向性のAB方式によるステレオ録音を軸としています。
ただし意図的に指向性のNOS方式を採用する場合もあります。
これらも専門的な知識は必要になりますが、無指向性を採用する主な理由はやはり空間の響きを直接デジタルデータに変換するというところにあります。
指向性マイクの場合は、演算処理によって常に計算されるベースとなる音源を録音するという感覚になりますが、対してAB方式の場合は、ステレオ感の調整、空間の振動もマニュアルで調整できるという利点があるわけです。
この時間差は、マイクロホン間の距離と音速を用いて計算することができます。
計算式
マイクロホン間の距離をdメートル、音速をcメートル/秒(空気中の音速は約343メートル/秒)とした場合、音源からマイクロホンに到達する最大時間差ΔΔtは以下の式で求められます。

この時間差によって、左右のマイクロホンに到達する音の位相差が生じ、ステレオ感が生まれます。
一般的に、この時間差が約1ミリ秒(0.001秒)を超えると、人間の耳はステレオとしての位置情報を感じ取ることができると言われています。
ステレオ感覚の飛躍
ステレオ感覚の飛躍とは、マイクロホン間の距離を変えることで得られるステレオイメージの変化を指します。
一般的な人間が感じるステレオ感覚では角周波数帯が一致、またはほぼ一致した状態になるのが常でしょう。
この間隔を変えていくことで(広げる)左右の広いステレオ感に加えて、時差による周波数の差(広がりがあればあるほど水面の輪は大きくなるのと同様に、周波数の輪も変化する)をわずかなビートとして感じられるようになります。
もちろん、これは、バイノーラルビートのような揺らぎはありませんが、制御すること意図するビートを録音技術を持って、アナログ的に産み出すことができるというわけなんです。
ただし、距離が広がるほど、ステレオ感は強くなりますが、あまりにも広がりすぎると、中央の音源が遠ざかったように感じられる「中央の空白」が発生する可能性があります。
こちらも、ヒーリング音響の場合は意図して空白を用意することもあります。
具体例
例えば、マイクロホン間の距離が0.5メートルの場合、最大時間差は以下のように計算できます。
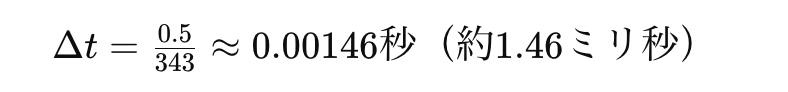
この場合、約1.46ミリ秒の時間差がステレオ感を生み出すというわけですね。
Pythonではこのようになります。
d = 0.5 # マイクロホン間の距離 [m]
c = 343 # 空気中の音速 [m/s]
# 最大時間差の計算
delta_t = d / c
print(f"最大時間差: {delta_t} 秒") # 約0.00146秒
金田式DC録音
DC録音では、直流(DC)を使用して音声信号を記録します。
この方法では、信号は時間と共に変化しない一定の電流として扱われます。
これは一般的な録音現場ではほとんど採用されることはありません。
金田明彦氏自らの手で特別にチューニングされたDC録音システムで録音することもあります。
しかし、それはかなり明確なDC録音の意図がある場合に限ります。
この辺りは明確に金田式と名乗るためには基盤からパーツすべてが統合された一つの生命体として機能する必要があり、ここでの解説は割愛します。
マスタリング技術
通常音源のリリースにはラウドネス調整という技術を使用しておりますが、Curanz Soundsではノーマライズ処理のみを基本方針としています。(例外はあり)
それは、やはり純粋に計算式でデジタル化されたデータに圧縮処理を加えたくないからです。
イメージする音、それはサンプリング音源の場所でも解説しましたが、生録の音になります。
ありのままの自然な音を目指してはいますが、教会音響のような特殊な音響が必要なコンセプトを持つアルバム制作の際には意図的に無理のない範囲で演算処理していき、音響をコントロールしています。
古代の叡智について
ピタゴラス含めて先人たちが残した古代の音の叡智。
これの解明にはかなり時間がかかります。
しかし、量子物理的なアプローチではある程度の解明は完了しています。
Curanz Soundsのピアノ小品集がなぜ人々を幸せにできるのか?
Curanz Soundsの祈願音源作品がなぜ本当に願いが叶うのか?
これには、古代の叡智が関わっているわけです。
これは宗教学的な話では収まらないまさにフィロソフィアの世界観と量子物理学の融合なのです。
今後も、叡智の研究レポートについては可能な範囲で公開していきます。
最後に
Curanz Soundsは聴いてくださるお客様の幸せが一番です。
Curanz Soundsの音源での体験談など是非コメント欄よりお寄せください。
みなさんの嬉しい声が制作の1番の栄養源になります。
世界中の人が音の叡智、音楽の神秘性を思い出し、取り戻し、幸せに満ちた人生、光に満ちた暮らしを送れますように。
今日もみなさまの幸せを祈りながら音楽を奏でます。
Curanz Sounds代表:朝比奈 幸太郎
