ピタゴラスは紀元前6世紀の古代ギリシャの数学者であり哲学者です。

彼の名前は今日でも特に「ピタゴラスの定理」として数学の教室で広く知られています。

しかし、ピタゴラスの影響は数学だけに留まりません。

彼の思想は哲学、音楽、そして宇宙の理解に深い足跡を残しました。

とりわけ音楽の分野では、ピタゴラス音律という現代では使われていない音律を開発しています。

なぜ現代では使われていないのか？

それは、あまりにも音、周波数の力が宇宙的で凄まじい神秘の力を持っているため、この叡智は危険であるとピタゴラス教団という秘密結社を設立し、その叡智を封じ込めてしまったからです。

これは史実ですので、我々21世紀に生きる音楽家はこの宇宙の叡智をどこまで解明していくのか？

取り戻していくのか？というのが重要な課題となります。

教団は絶対秘密主義で、内部情報を外部に漏らすことを厳しく禁じており、違反した者は船から海に突き落として死刑にしているほどです。

『ただしこれは諸説あり、史料によっては、無理数の存在を知ったピタゴラス教団は動揺し、この発見を口外しない誓いを立てあい、無理数の存在を隠蔽しようとしましたが、ヒッパソスという名の男が反発し、あくまで事実を公表しようとしたため、教団は彼を海に突き落としたとする説もあります。』

そのため教団内部の研究記録や、ピタゴラス本人の著作物は後世に一点も伝わっていません。

このことから、伝わっている数学や定理は秘密にする必要もないほど他愛のないこと・・・であると推察できます。

本記事では、ピタゴラスの生涯、彼の教え、そして彼が設立した教団について詳しく掘り下げていきます。

読者の皆さんはピタゴラスの数学的業績だけでなく、彼の哲学的見解や教団内での生活についても理解を深めることができるでしょう。

ピタゴラスの生涯

（古代ギリシャ語: Πυθαγόρας, ラテン文字転写: Pȳthagórās[1]、ラテン語: Pythagoras、英: Pythagoras、紀元前582年 – 紀元前496年）

ピタゴラスは紀元前570年頃、エーゲ海に浮かぶ現在のトルコ沿岸にあるイオニア地方のサモス島で、宝石細工師の息子として生まれた。

近くの町には、やはり著名な数学者のタレスが住んでいたと言われています。

彼の生涯については多くの伝説があり、事実と虚構が混在しているため、彼の実際の生涯について正確に知ることは難しいです。

彼の肖像や彫像類も、すべて後世の伝聞や想像で作られたイメージであり、実際にどういう風貌をした人物だったかも不明なのです。

旅多きピタゴラスの青年期

若き日のピタゴラスは広範な知識を求めて多くの国を旅したと伝えられています。

伝記によると、古代オリエント世界の各地を旅しており、エジプトでは幾何学と宗教の密儀を学び、フェニキアで算術と比率、カルデア人（バスク語版）から天文学を学んだといわれています。

ポルピュリオスなどの伝記によれば、ゾロアスター教の司祭のもとで学んだともいわれています。

さらにはイギリスやインドにまで旅したという伝説まであるほどの旅多き青年期でした。

秘密結社の設立へ

彼は約20年旅を続けました。

故郷のサモス島に戻り、ピタゴラス学派を立ち上げたのです。

しかし、当時のサモスは僭主ポリュクラテスの抑圧支配下にあり、学問研究に意識が向いていなかったので、イタリア半島の植民市に移住し立ち上げたとされています。

この教団はやがて地域の有力者の保護を受けながら大きな力を持つようになりました。

数百人以上の信者を集めつつ、ピタゴラスは当時弟子だったテアノという女性と結婚しています。

ところが、当時教団を支援していた地域の有力者が政争に巻き込まれて失脚。

このときにかつて教団への加入を希望したがテストで落とされて門前払いになった人物が、その遺恨から市民を扇動し、教団は暴徒と化した市民に焼き打ちされて壊滅。

ピタゴラスも殺されたと伝えられています。

教団に入るための入会試験

テストで落とされて門前払いになった人物が、その遺恨から市民を扇動したとありますが、教団に加わるためには、当時、数学の難しい試験に合格する必要があり、数学に秀でた人だけが選ばれました。

その結果この教団は、古代世界で非常に有名な数学研究グループとなったわけです。

彼らは数字の10を完璧な数と見なし、10個の点を三角形に配置した「テトラクテュス」というシンボルを使用していました。

ピタゴラスや彼の教団は多くの数学的定理を発見しましたが、これらがピタゴラス自身のものなのか、教団の他のメンバーの成果なのかを区別するのは難しいのが現実です。

これらの成果の多くは、後にユークリッドの『原論』に収められています。

ピタゴラスが有名な定理を発見した時、彼は神に牡牛を捧げたという詩がありますが、どの定理かははっきりしていません。

また、教団の規則を考えると、本当に牡牛を捧げたかも疑問です。

いくつかの説では、これがピタゴラスの定理を指すとしていますが、明確な証拠はありません。

ピタゴラスは、数の調和や整合性を非常に重んじ、完全数や友愛数などを宗教的に崇拝しました。

しかし、教団の一員が無理数を発見した時、その存在を認める代わりに、発見者を死刑にしたとされています。

これは、彼らの信念にとって受け入れがたいものだったからです。

ピタゴラスの哲学は、二元論に基づき、現象世界を解析するための十項目の対立項を提案しました。

彼の数学や輪廻転生に関する考え方は、プラトンにも大きな影響を与えています。

アリストテレスも『形而上学』でこれらの対立項を取り上げ、ピタゴラスがオルペウス教から影響を受け、輪廻を説いたと記しています。

ピタゴラスの哲学〜この宇宙の仕組み

ピタゴラスの哲学の中心に、「万物は数である」という考えがあります。

彼にとって、数は単なる算術や計算の道具ではなく、宇宙の本質的な構成要素であり、自然界の調和、比例、秩序を理解する鍵でした。

この哲学的見解は、後に「数の神秘主義」と呼ばれるようになります。

数の神秘主義

ピタゴラスは、数が持つ神秘的な性質と力を深く信じていました。

例えば、彼は音楽の調和が数学的比率によって説明できることを発見し、これを宇宙の秩序を理解するためのモデルとして確立。

弦楽器の弦を振動させる実験（後述します）を通じ、音の高さが弦の長さの数学的比率によって決定されることを示し、この発見は「調和の数理」と称されるようになりました。

宇宙観と自然界における調和

ピタゴラスは、宇宙が数によって秩序付けられており、すべてのものが数学的な調和に基づいて組み立てられていると考えました。

天体の運行から日々の生活に至るまで、全てが数の法則に従っているというこの観点は、彼の哲学的思考と実践の基礎を形成しました。

ピタゴラスとその追随者たちは、この宇宙の調和を理解し、その法則に従うことが、道徳的な生活を送る上での最も重要な要素であると信じていました。

道徳と政治における応用

ピタゴラスの数の哲学は、個人の道徳生活や政治思想にも深く影響を与えました。

彼は、人間の魂もまた数学的な調和に従って成長し、発展すると考え、この理念は彼の教団の日常生活や習慣にも反映されました。

共同生活、財産の共有、植物性食品の摂取など、ピタゴラス教団の実践は、宇宙の調和と一致するように設計されていました。

また、彼は政治社会における正義と調和を実現するために、数学的原理を応用することの重要性を説いたとされます。

ピタゴラスの哲学は、彼自身と彼の教団によって生み出された数多くの数学的、音楽的な発見と密接に結びついています。

ピタゴラスの音楽実験

ピタゴラスが行った弦楽器の弦を振動させる実験は、後に西洋音楽理論の基礎ともなる重要な発見につながっています。

この実験を通して、ピタゴラスは音楽の調和が数学的比率によって説明できることを示しました。

以下にその実験の詳細とその意義について解説します。

音楽理論と宇宙の調和への貢献

ピタゴラスは音楽の基本的な音程が特定の数比に対応することを発見しました。

彼はオクターヴ（8度）を2対1、完全五度を3対2、完全四度を4対3、そして全音（2つの音程の差）を9対8の比率で定義しました。

鍛冶屋の前を通りかかった時、ピタゴラスはハンマーの共鳴する音が快い和音を作っていることに気づき、中を調べると、ハンマーの音程がその重さの比率と関係していることを発見しました。

5本のハンマーのうち4本は「12 : 9 : 8 : 6」という単純な数比で関係していましたが、残りの1本は不協和音を生み出したのです。

（この比率は実際には弦の長さには適用できるものの、ハンマーの重さには当てはまりません。）

さらに、ピタゴラスは続けて弦楽器や笛で実験を行い、弦の長さの比が音程を決定することを発見しました。

彼はこの発見を確認するために、モノコードという調律道具を発明しています。

宇宙の周波数を解明

ピタゴラスはまた、「天球の音楽」という理論も提唱しています。

これは、各惑星が特定の音に対応し、それらが調和を成すという考えです。

このことは、現代ではNASAの調査によって、この地球の振動数そして、それらを数学的に共振させるための倍音などは定義されています。

詳しくはこちらの記事。

イタリアでの432hz研究〜心拍数を下げる効果と地球の振動すについて

ピタゴラス音律は、周波数比が3対2の音程を基にした音律で、これは中国の三分損益法に似ています。

ピタゴラスコンマは、ピタゴラス音律での異名同音（異なる名前を持ちながら同じ音高を示す音）の微妙な差を指します。

ピタゴラス音律の基本

ピタゴラス音律は、純正な完全五度（周波数比3:2）を積み重ねて他の音を導き出す方法に基づいています。

• 完全五度の積み重ね：ピタゴラス音律では、基音から完全五度上の音を12回積み重ねることにより、12音を生成します。ただし、この方法では微妙な調整が必要であり、12回の完全五度を積み重ねて得られる最後の音は、基音のオクターヴ上の音と完全に一致しない（ピタゴラスコンマ）という問題が生じます。
• 数学的純度と実践上の問題：数学的に純粋な関係に基づくため、和音の響きは非常にクリアで美しいですが、全ての調で同じ純度を保つことができません。これは特にキーが離れた調での演奏において不協和音を引き起こす可能性があります。

ピタゴラス音律は、西洋音楽における調律法の発展に大きな影響を与えましたが、ピタゴラスコンマの問題や他の調での演奏時の不協和音の問題を解決するため、平均律などの他の調律法が発展しました。

平均律についてはこちらの記事で触れています。

バッハと神〜バッハの音楽を軸とした宗教音楽の研究

ちなみにピタゴラス音律と純正律はまた違う音律ですので、注意してください。

純正律は、完全五度だけでなく、主要三度（周波数比5:4）や他の音程も純正な比率で調整しています。

これは、和音の純度を最大限に高めることを目的としており、特に主要三度の和音が非常に清らかに響きます。

音楽家ならではの深掘り

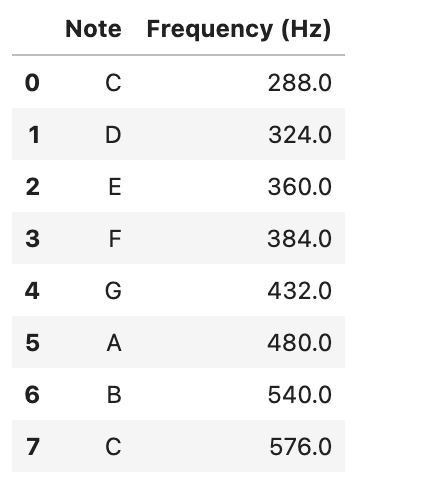
ピタゴラス音律をCメジャースケールにて音程感覚を表で示すことで、その数学的な関係性を明確に理解できます。

ピタゴラス音律では、完全五度（周波数比3:2）の積み重ねに基づいて音階が構築されますが、ここでは、Cを基準音として、ピタゴラス音律によるCメジャースケールの各音とその周波数比を計算し、表にまとめてみましょう。

基準となるCの音（例えば、C4 = 256Hz）から出発し、完全五度の関係を用いて他の音を導出。

ただし、実際の計算ではオクターヴ調整を行う必要があることに注意してください。

ピタゴラス音律では、12の完全五度を積み重ねると基準のオクターヴよりもわずかに高い音（ピタゴラスコンマによる差）になりますが、ここでは簡略化のためにこの微細な差は無視して、Cメジャースケールの音程を紹介します。

それでは、Pythonを使用して、Cメジャースケールにおけるピタゴラス音律の各音の周波数比を計算し、表形式で表現しましょう。

サンプルコードをコメントアウトで解説しながら掲載しておきます。

計算自体はpandasを使用していますが、matplotlibなどで自由にプロットしてみてください。

import pandas as pd

# ピタゴラス音律における音程の周波数比を計算
# Cメジャースケールの音程名
notes = ['C', 'D', 'E', 'F', 'G', 'A', 'B', 'C']

# ピタゴラス音律では、完全五度の周波数比は3:2
# 各音程までの完全五度のステップ数 (Cからの距離)
# Cからのステップ数を計算することで、各音のピタゴラス音律における位置を決定
steps_from_c = [0, 2, 4, -1, 1, 3, 5]

# 周波数比の計算
# Cを基準とし、それぞれの音に対して完全五度を積み重ねる（必要に応じてオクターヴ調整）
# オクターヴ調整は % 2 を用いて実現（1オクターヴ上の音は周波数が2倍になるため）
ratios = [(3/2) ** step % 2 for step in steps_from_c]
# Cのオクターヴ調整
# 最後のCは基準のCのオクターヴ上なので、周波数比は2となる
ratios.append(2.0)

# DataFrameで結果をまとめる
# DataFrameを使用して結果を表形式で整理し、可読性を高める
df = pd.DataFrame({
    'Note': notes,
    'Steps from C': steps_from_c + [7],  # Cのオクターヴは7ステップ上
    'Frequency Ratio': ratios
})

# 結果の表示
# 最終的なDataFrameを表示し、各音の周波数比を確認
print(df)

ピタゴラス音律と432hzのPythonコード

import pandas as pd

# 432Hzを基準とするピタゴラス音律の計算
base_frequency = 432  # Aの周波数 (Hz)

# A4からC4への周波数比（ピタゴラス音律における完全四度下）
# ピタゴラス音律では、A4からC4へは完全五度を9回下がってオクターヴを調整
c4_frequency_from_a4 = base_frequency / (3/2) ** 5

# Cメジャースケールでの音名と、それぞれの音に対するピタゴラス音律に基づくステップ数
# Cから各音までの完全五度の積み重ねを表す
steps_from_c_pythagorean = [0, 2, 4, -1, 1, 3, 5, 7]  # Cからのステップ数

# 各音の周波数を計算
frequencies_pythagorean_corrected = [c4_frequency_from_a4 * (3/2) ** step for step in steps_from_c_pythagorean]
# オクターヴ調整: 各音の周波数が432Hzを超えないように調整
frequencies_pythagorean_corrected = [freq / 2 ** int(freq / base_frequency) for freq in frequencies_pythagorean_corrected]

# 結果をDataFrameでまとめる
df_pythagorean_corrected = pd.DataFrame({
    'Note': notes_just,
    'Pythagorean Tuning Frequency (Hz) Corrected': frequencies_pythagorean_corrected
})

df_pythagorean_corrected

このコードは、ピタゴラス音律の原則に基づいて、特定の基準周波数（この場合は432Hz）からCメジャースケールの各音の周波数を計算しています。

最終的に、各音の周波数をDataFrameにまとめて表示し、ピタゴラス音律におけるCメジャースケールの構造を理解するのに役立ちます。

純正律の計算コードも一応メモしておきましょう。

import pandas as pd

# 純正律に基づくCメジャースケールの音程名と周波数比
notes_just = ['C', 'D', 'E', 'F', 'G', 'A', 'B', 'C']
ratios_just = [1/1, 9/8, 5/4, 4/3, 3/2, 5/3, 15/8, 2/1]

# 結果をDataFrameでまとめる
# ここでは、各音程名とその純正律における周波数比をDataFrameに格納しています
df_just = pd.DataFrame({
    'Note': notes_just,
    'Just Intonation Frequency Ratio': ratios_just
})

# DataFrameの出力
# 最終的にまとめたDataFrameを出力し、各音の純正律に基づく周波数比を確認します
print(df_just)

432hzと純正律のPythonコード

# 432Hzを基準とする純正律の計算
base_frequency = 432  # A4の周波数

# A4からC4への周波数比（純正律における完全四度下）
a_to_c_ratio = 4/3

# C4の周波数を計算
c4_frequency = base_frequency * a_to_c_ratio / 2  # オクターヴを1つ下げる

# 純正律におけるCメジャースケールの周波数比
ratios_just = [1/1, 9/8, 5/4, 4/3, 3/2, 5/3, 15/8, 2/1]

# 各音の周波数を計算
frequencies_just = [c4_frequency * ratio for ratio in ratios_just]

# 結果をDataFrameでまとめる
df_just_432 = pd.DataFrame({
    'Note': notes_just,
    'Frequency (Hz)': frequencies_just
})

df_just_432

A4の周波数を432Hzとした場合、純正律でC4からスタートしてG4までの関係を計算する際、G4が432Hzになるのは、A4がこのスケールにおけるG4の位置にあるからです。

つまり、A4（432Hz）がGの音に対応しており、このスケールでGが432Hzとなっているのはそのためです。

ただし、実際にはC4からスタートしてG4に至るまでには純正律の比率を適用し、それによって各音の周波数を導出してください。

特定の音高（この場合はA4）を基準として他の音高を定義しているからです。

ピタゴラス教団の発見した叡智まとめ

ピタゴラス教団が発見したり、大きく貢献した叡智や知識は、数学だけに留まらず、音楽、天文学、哲学、科学の基礎など多岐にわたります。

以下に主要な貢献をリストアップしますが、古代ギリシャ時代の記録の性質上、これらの発見がピタゴラス自身や彼の直接の弟子たちによるものか、教団の後継者によるものかは明確ではない場合もあります。

数学

1. ピタゴラスの定理: 右角三角形の辺の関係を示す定理。三角形の直角を挟む二辺の長さの二乗の和は、斜辺の長さの二乗と等しい。
2. 無理数の発見: √2が無理数であることの発見は、数の概念を根本から見直す契機となった。
3. 数の比率に基づく幾何学の研究: 形と数の関係性に深く焦点を当て、後のユークリッド幾何学の基礎を築いた。

音楽

1. 音楽の数学的比率の発見: 音楽の調和が弦の長さの数学的比率によって決まることを発見し、西洋音楽理論の基礎を築いた。
2. 音階の構築: 音楽と数学の関係性を用いて、音階を理論的に構築。

哲学・宗教

1. 万物の数理: 「万物は数である」という哲学的見解を提唱し、世界を数学的原理で理解しようとした。
2. 魂の不死: 魂の不死と輪廻転生を信じる教義を広めた。

科学・天文学

1. 宇宙の調和: 天体が数学的な調和に基づいて動いているとする「音楽の宇宙」の概念を提唱。
2. 地球球体説: 地球が球形であることについての考察（この点については、ピタゴラス教団と直接関連づけられる記録は限定的ですが、後のギリシャ哲学に影響を与えた）。

生活・倫理

1. 共同体生活: 共有財産、共同生活を実践し、精神的な純粋さを目指した。
2. 食生活: 肉食を避けるなど、倫理的な食生活を奨励。

ピタゴラス教団のこれらの発見や教えは、古代ギリシャの思想や科学に深い影響を与え、西洋文化の発展に寄与しました。彼らの叡智は、直接的な発見や考え方だけでなく、後世の学問や思想に対するアプローチの仕方にも影響を及ぼし続けています。

魂の不死に関して

ピタゴラス教団における魂の不死と輪廻転生の教えは、ピタゴラス哲学の核心部分をなし、彼らの生活様式や倫理観に深く影響を与えていました。

ピタゴラスと彼の教団は、魂が不滅であり、肉体的な死後も存続するという信念を持っていました。

彼らによれば、魂は宇宙の根本原理の一部であり、物質的な世界を超越した存在であるとされます。

輪廻転生

輪廻転生の概念は、魂が一つの肉体から別の肉体へと生まれ変わるという教えです。

ピタゴラス教団は、魂が完全なる知識と調和の状態に達するまで、この過程を繰り返すと考えていました。

この教えは、個人の行動が魂の進化に直接影響を与えるという倫理的な意味合いを持ちます。

つまり、善行を積むことで魂はより高い形態へと進化し、悪行はその進化を妨げるとされていました。

ちなみにピタゴラスの前世はエウポルボスであると自ら語っていたと言われています。

生活と倫理への影響

魂の不死と輪廻転生の教えは、ピタゴラス教団のメンバーの日常生活にも深く反映されていました。

例えば、彼らは肉食を避け、生命を尊重する食生活を実践していました。

これは、全ての生命が魂を宿しており、それを尊重する必要があるという信念に基づいています。

また、正直さ、自制心、相互の尊重などの道徳的価値も、この宇宙観と密接に関連していました。

この考え方は後にプラトンのイデア説などに繋がっていきます。

Note	Steps from C	Frequency Ratio
C	0	1.000
D	2	1.125
E	4	1.265625
F	-1